티스토리 뷰
1. 그래프 개념
[그래프 용어 정리]
- 목적: 출발지, 목적지를 정하고 그에 맞는 최적의 경로를 구하기
- ex) 지도, 지하철 노선도 최단 경로, 전기 회로의 소자들, 도로(교차점과 일방 통행길)

그래프: 노드와 간선으로 이루어진 자료 구조.(1, 2, 3)
- 노드 (Node, Vertex)
- 간선 (Edge): 정점간의 관계를 나타낸다.
- G = (V, E)로 나타낸다.
- 경로 (Path): 시작점에서 도착점으로 가는 간선의 연속된 것 (2 -> 3 -> 1)
- 사이클: 정점 A에서 다시 A로 돌아오는 경우 ( A -> B -> D)단순 경로와 단순 사이클
- 경로/ 사이클에서 같은 정점을 두 번 이상 방문하지 않는 경로/ 사이클
- DAG (Diredcted Acyclic Graph)
- 사이클이 없는 그래프. 트리(Tree)가 대표적인 DAG이다.
- 가중치 (Weight): 간선에 가중치가 있는 경우
- A에서 B로 이동하는 거리, 이동하는데 필요한 시간, 이동하는데 필요한 비용 등등...
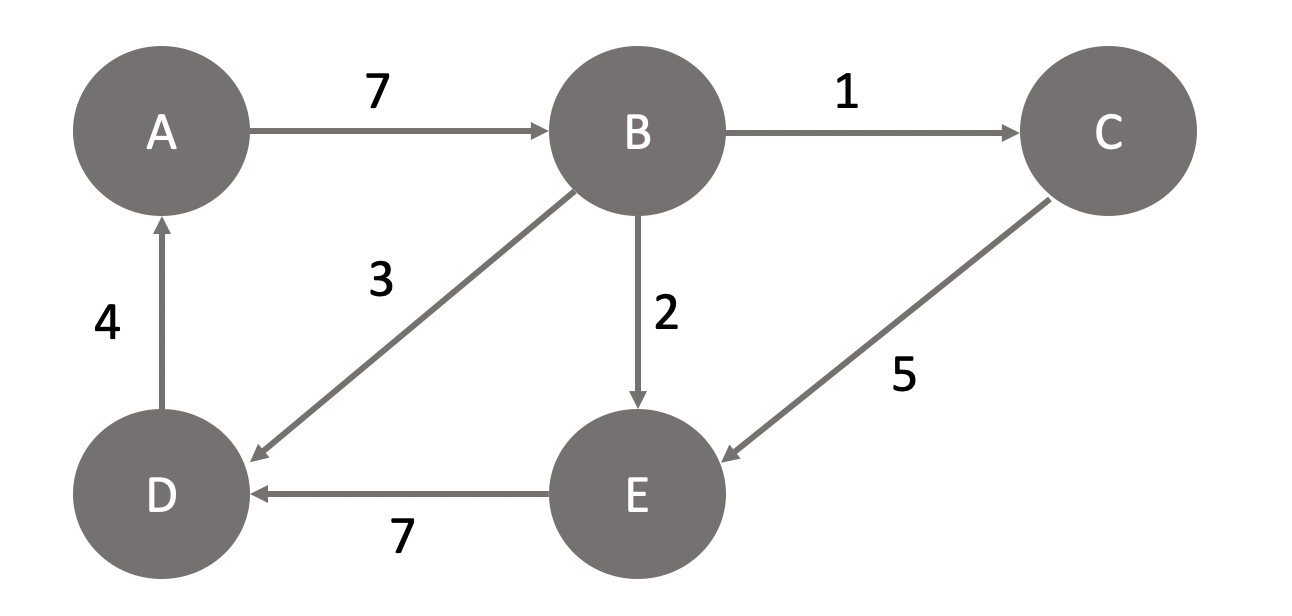
- 차수 (Degree): 정점과 연결되어 있는 간선의 개수
- A의 차수: 2, D의 차수: 3
- 진입 차수 (In-degree): 방향 그래프에서 정점으로 들어오는 간선의 수
- ex) D의 In-degree: 2개
- 진출 차수 (Out-degree): 방향 그래프에서 정점에서 나가는 간선의 수
- ex) D의 Out-degree: 1개
[그래프 종류]
- 무방향 그래프(undirected graph): 간선에 방향표시가 없다.
- 무방향 그래프는 간선을 통해 양방향으로 이동할 수 있다.
- (A, B)와 (B, A)는 동일
- ex) 양방향 통행 도로
- 방향 그래프(directed graph), 다이그래프(digraph): 간선에 방향표시가 있다.
- 간선에 방향이 존재하는 그래프
- A -> B로만 갈 수 있다. <A, B>로 표현 가능
- <A, B>와 <B, A>는 다름
- ex) 일방 통행
- 가중치 그래프 (Weight Graph): 간선에 가중치 정보를 두어서 그래프를 구성
- 두 정점 사이의 거리, 두 정점을 이동하는데 걸리는 시간 등을 표현
- ex) 도시 간에 이동할 때 최단 시간을 구하는 문제
- 완전 그래프 (Complete Graph): 그래프의 정점이 다른 모든 정점과 연결된 그래프
- 무방향 완전 그래프
- 정점 수: n이면 간선의 수: n * (n-1) / 2
- 방향 완전 그래프
- 정점 수: n * (n-1)
- 무방향 완전 그래프
- 부분 그래프 (Sub Graph): 원래그래프의 일부 정점, 간선으로 구성된 그래프


[그래프의 표현]
1. 인접 행렬 (Adjacency Matrix)
- 정점의 개수를 V라고 했을 때 V*V 크기의 이차원 배열을 이용함
- i -> j로의 간선이 있을 때 Matrix[i][j] = 1, 없을 때 Matrix[i][j] = 0


무방향 그래프는 (A, B), (B, A)가 같은 간선이기 때문에 대칭 행렬 (Symmetric Matrix)를 이룬다.
방향 그래프가 대칭 행렬이 되려면 완전 그래프여야 된다.
<인접 행렬 구현>
package graph;
import java.util.Arrays;
import java.util.Scanner;
public class AdjacencyTest {
static int E;
static int V;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
V = sc.nextInt();
E = sc.nextInt();
int[][] ad = new int[V+1][V+1]; // Vertex의 이름을 그대로 사용하기 위해 (V+1)(V+1)개만큼 배열 생
for(int i=0; i<E; i++) {
int _i = sc.nextInt();
int _j = sc.nextInt();
ad[_i][_j] = ad[_j][_i] = 1; // 1대신 가중치를 넣으면 가중치 그래프
}
for(int i=0; i<V+1; i++) {
System.out.println(Arrays.toString(ad[i]));
}
}
}

2. 인접 리스트 (Adjacency list)
- 각 정점마다 연결된 간선들의 연결 리스트를 갖는 방식으로 구현
- A[i]에는 i와 연결된 정점들 (간선)을 리스트로 포함하고 있음
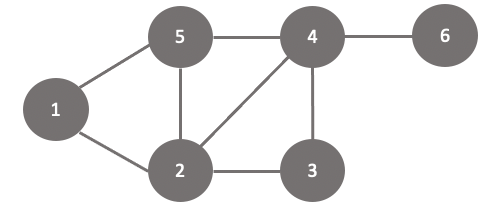

인접리스트에서 연결된 정점의 순서는 중요하지 않다.
인접리스트를 저장할 때 동적인 배열이 필요하다. 한 정점과 연결될 간선의 수를 모르기 때문이이다.
자바에선 LinkedList, ArrayList 등으로 구현하고 C++에선 vector를 사용해서 구현한다.
가중치를 갖는 방향 그래프를 연결그래프로 구현하기 위해선 (정점, 가중치) 페어 형식으로 저장해야 한다.
<인접리스트 구현>
package graph;
import java.util.ArrayList;
import java.util.Scanner;
public class AdjacencyListTest {
static int V;
static int E;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
V = sc.nextInt();
E = sc.nextInt();
// 이중 arrayList를 만들어줌
ArrayList<ArrayList<Integer>> ad = new ArrayList<ArrayList<Integer>>();
//1차원 ad 리스트 초기화
for(int i=0; i<V+1; i++) {
ad.add( new ArrayList<Integer>() );
}
for(int i = 0; i<E; i++) {
int _i, _j;
_i = sc.nextInt();
_j = sc.nextInt();
ad.get(_i).add(_j);
ad.get(_j).add(_i);
}
for(int i = 1; i <= V; i++) {
System.out.print("정점 " + i );
for(int j = 0; j < ad.get(i).size(); j++) {
System.out.print(" -> " + ad.get(i).get(j));
}
System.out.println();
}
}
}

인접행렬 vs 인접리스트
두 가지 방식은 완전히 정반대의 특성을 가짐. 하나의 단점이 다른 방식의 장점이기 때문에 구현하려는 알고리즘 종류나 그래프 종류에 따라 적절하게 사용해야 함
- 공간 복잡도
- 인접 행렬: O(V*V)
- V개의 Node를 표현하기 위해 V * V개만큼 공간이 필요
- 인접 리스트: O(V+E)
- V개의 리스트에 간선 E개만큼 원소가 들어있다.
- E의 개수가 V^2이 되지 않는 이상 보통 V+E <<<<<<<<< V^2 이므로 인접리스트의 공간 복잡도가 훨씬 낮다. 그러나 보통 그래프에선 간선의 개수가 정점의 개수보다 훨씬 작으니 인접리스트의 공간복잡도가 인접 행렬보다 훨씬 작다.
- 인접 행렬: O(V*V)
- 시간 복잡도
- 인접 행렬
- 간선 존재 여부 확인: O(1) - 정점 u, v가 주어졌을 때 A[u][v] 으로 한번의 접근만에 두 노드의 연결 여부를 파악할 수 있어서 굉장히 빠르다.
- 주위 연결 노드 확인: O(V*V) - 주변 연결된 노드를 찾을 땐 행렬을 전부 탐색해야 하므로 O(V^2)이다. 엄청 느리다.
- 인접 리스트
- 간선 존재 여부 확인: O(E) - 정점 u의 연결리스트 원소를 전부 찾아봐야 한다.
- 주위 연결 노드 확인: O(E) - 이것도 정점 u에 연결된 리스트를 보기만 하면 된다.
- 인접 행렬
- 결론
- 인접 행렬
- 그래프에 간선이 많이 존재하는 밀집 그래프 (Dense Graph) 의 경우 유리하다.
- 장점: 두 정점을 연결하는 간선의 존재 여부를 ad[v][u] O(1)만에 알 수 있음
- 단점: 어떤 노드에 인접한 노드를 찾기 위해선 모든 노드를 전부 순회해야 함
- 인접 리스트
- 그래프에 간선이 많지 않은 희소 그래프 (Sparse Graph) 의 경우 유리하다.
- 장점: 어떤 노드에 인접한 노드를 쉽게 찾을 수 있다.
- 단점: 간선의 존재 여부와 정점의 차수를 구하려면 정점 u의 리스트에 연결되어 있는 노드의 수만큼 시간이 걸린다.
- 인접 행렬
'Data Structure' 카테고리의 다른 글
| [자료구조] 트리, 이진트리, 힙 - 2 (0) | 2021.02.15 |
|---|---|
| [자료구조] 트리, 이진트리, 힙 - 1 (1) | 2021.02.15 |
| [CS 면접질문 대비] 그래프 및 자료 구조 (0) | 2021.01.31 |
| [자료구조] BFS (0) | 2021.01.31 |
| [자료구조] DFS (0) | 2021.01.30 |
댓글
