티스토리 뷰
[그래프의 탐색]
그래프의 모든 정점을 한번씩 탐색하기 위해 BFS, DFS 알고리즘이 개발되었다.
- 깊이 우선 탐색 Depth First Search : DFS
- 넓이 우선 탐색 Breadth First Search: BFS
1. DFS
한 정점에서 갈 수 있는데까지 완벽하게 탐색하는 방법이다. 한 정점에서 이동 가능한 다음 정점으로 이동하고, 다시 다음 정점에서 연결된 노드를 탐색하는 알고리즘이다. 더이상 갈 수 없으면 뒤로 돌아올 수 있도록 현재 위치를 스택(Stack)에 저장해야 한다.
- 필요한 것
- 스택: 현재 어떤 정점에서 탐색하는지 추적
- 배열: 정점의 방문 여부를 체크
<DFS의 특징>
- DFS는 Stack을 사용하여 구현하는 방법과 재귀 호출로 구현하는 방법이 있다.
- DFS를 구현할 때, 어떤 노드를 방문했었는지 여부를 반드시 검사해야한다. 그렇지 않으면 무한루프에 빠질 수 있다.
- DFS의 시간 복잡도
- 인접 행렬 그래프: O(V+E)
- 인접 리스트 그래프: O(V*V)
- E > V인 희소 그래프(Sparse Graph)의 경우 인접 리스트가 유리
- 장점
- 현 경로상의 노드만 기억하면 되므로 그래프 높이 만큼의 공간만 요구
- 목표노드가 깊은 단계에 있으면 해를 빠르게 구할 수 있음
- 단점
- 얻어진 해가 최단 경로가 된다는 보장이 없다. (DFS는 목표에 이르면 탐색을 끝내버리므로, 이 때 얻어진 해가 최적이 아닐 수 있다.)
<DFS의 탐색 과정>

위 그래프를 1부터 탐색하겠다.


1. 1을 방문, 스택에 1을 넣음


2. 1과 연결된 2로 간다. 스택에 2를 넣고 Checked 배열에 2를 방문했다고 기록.


3. 2에서 갈 수 있는 정점은 1, 5, 3임. 그런데 1은 이미 방문했기 때문에 3 방문한다. 현재 정점은 3이고 스택에 3을 넣는다. checked 배열에 3 방문 true로 기록.


4. 현재 정점 4. 스택에 현재 정점인 4를 넣는다.
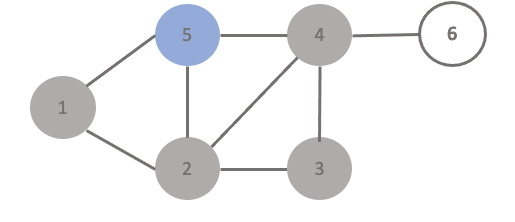

5. 현재 정점 5. 현재 스택에 5를 넣는다.


6. 그 다음 5에서 갈 곳을 찾았는데 주변 정점 전부 방문함. 이 때 스택에서 5를 제거하고 4로 돌아감. 정점 4에서부터 다시 노트 탐색. (4에서 다시 시작)


7. 4에서 방문 안한 정점을 찾아 6을 방문. 스택에 6 넣음. 그래프의 모든 정점을 방문했으므로, 그래프 탐색을 종료함.
<인접리스트로 구현한 DFS>
package graph;
import java.util.ArrayList;
import java.util.Scanner;
public class DFS {
static int E;
static int V;
static boolean[] visited;
static ArrayList<ArrayList<Integer>> ad;
public static void dfs(int u) {
visited[u] = true;
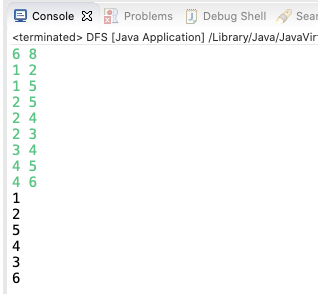
System.out.println(u);
for(int v : ad.get(u)) {
if(!visited[v]) {
dfs(v);
}
}
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
V = sc.nextInt();
E = sc.nextInt();
ad = new ArrayList(V+1);
visited = new boolean[V+1];
for(int i=0; i<V+1; i++) {
ad.add(new ArrayList<>());
}
for(int i=0; i<E; i++) {
int u = sc.nextInt();
int v = sc.nextInt();
ad.get(u).add(v);
ad.get(v).add(u);
}
dfs(1);
}
}
'Data Structure' 카테고리의 다른 글
| [자료구조] 트리, 이진트리, 힙 - 2 (0) | 2021.02.15 |
|---|---|
| [자료구조] 트리, 이진트리, 힙 - 1 (1) | 2021.02.15 |
| [CS 면접질문 대비] 그래프 및 자료 구조 (0) | 2021.01.31 |
| [자료구조] BFS (0) | 2021.01.31 |
| [자료구조] 그래프(Graph) 개념 (1) | 2021.01.30 |
댓글
